mol-ellipsize: Python package for calculating the size of molecules

Fit an ellipsoid to points to calculate their size

Acknowledgements

This work was done under the supervision of A/Prof. David Huang and Prof. Christian Doonan. I was supported by an Australian Government RTP Scholarship and a PhD top-up scholarship from CSIRO Division of Materials Science and Engineering. I would like to thank Dr Jesse Teo, Dr Natasha Maddigan, Dr Weibin Liang, Dr Justin Spence, A/Prof Stephen Bell, Dr Austin Mroz and Dr Kim E. Jelfs for discussions about this work.

Why?

I wrote mol-ellipsize as part of my final PhD project, in which we aimed to screen molecules for diffusion through metal-organic frameworks based on their size. We were targetting molecule databases containing > 10,000 molecules and wanted an automated, high-throughput evalutor of molecular size that also considered the flexibility of molecules. From what I found at the time, it was common to evaluate the size of moleules by manually measuring distances or treating them like a cylinder (webster1998, polyukhov2019). However, I found no code that could automate this to handle many conformers of many molecules. Therefore, I wrote mol-ellipsize… Well, I actually wrote a lot of code that collected and analysed those molecules from databases, but I do not need all that mess anymore (it is on my github!) and thought mol-ellipsize would be a neat, useful package.

mol-ellipsize is a Python package easily installable through pip install mol-ellipsize. RDKit is required for most of the molecule handling.

How?

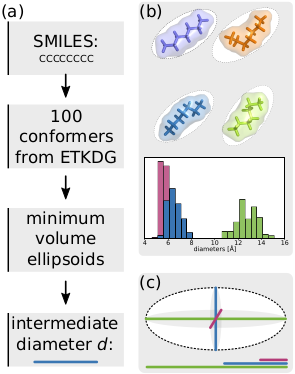
mol-ellipsize contains two main classes: one to define molecules and their shape, and another to fit an ellipsoid to that shape. Given an ellipsoid, the size of a molecule (or any shape!) is determined by the three axes/diameters of that ellipsoid. For a molecule diffusing through a pore, the second diameter is the one that matters.

Molecules are mostly handled using RDKit, which allows for the generation of conformers with the ETKDG algorithm. We can consider flexibility of molecules by calculating the size of many conformers. RDKit provides methods for calculating the shape of a molecule on a grid based on the vdW radii of each atom. The points inside the vdW cloud of the molecule are the input into the ellipsoid fitting algorithm. mol-ellipsize simplifies this whole process by taking in an RDKit molecule and handling all intermediate steps.

mol-ellipsize calculates the minimum-volume enclosing ellipsoid (shown schematically in black in the figure below, b) for the points in the vdW volume of each conformer using a minimization algorithm based on the Khachiyan algorithm (we used a tolerance of 0.1 for the relative change in the solution as a stopping criterion) (moshtagh). The code for ellipsoid fitting was taken from this GitHub repository. I personally need a better grasp on mathematics to understand the fitting algorithm, but it basically treats the problem as a minimisation of the volume of the ellipsoid covering the points.

The whole process using RDKit looks something like this:

Examples and limitations.

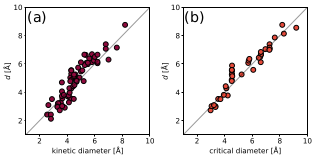
We have parameterised our algorithm, most importantly the vdW radii, using a test-set of kinetic diameters for small molecules. For molecular size, we use the minimum intermediate diameter ($d$) of all conformers of a molecule. We expect the limitations to come about for very large (this would also be very slow and memory intensive!) and flexible molecules, where the number of conformers needed to be sampled increases or ETKDG fails. The parity plots below summarise the agreement with kinetic diameters - more details are available in here (JOSS paper format). The defaults in mol-ellipsize are based on this parameterisation. Users should consider the trade-off between accuracy and computational efficiency.

The final thing to show is that the EllipsoidTool can be used on arbitrary coordinates. For example, the code below takes a pore from an xyz file output by PoreMapper and fits an ellipsoid to it.

# Code example of arbitrary coordinates.

# Read XYZ coordinates.
coordinates = []
with open(pore, 'r') as f:
    for line in f.readlines()[2:]:
        elem, x, y, z = line.rstrip().split()
        coordinates.append([float(x), float(y), float(z)])
coordinates = np.array(coordinates)

# No settings needed, but vdw radii not considered.
ET = mes.EllipsoidTool()
center, radii, rotation = ET.get_min_vol_ellipse(coordinates)
print(f'{pore_name} with radii: {radii}')

More example uses are available as part of my YouTube tutorials:

What next?

It is available on GitHub with a series of examples are provided here.

Please, test it, use it, break it and send me feedback!